����ֱ��

Dalam kehidupan sehari-hari, banyak aktivitas atau kegiatan yang terkait dengan transformasi geometri. Transformasi geometri terdiri dari translasi, refleksi, dilatasi, dan rotasi. Pada artikel ini akan dibahas tentang rumus refleksi dan contohnya.

Salah satu contoh penerapan transformasi geometri yang sering kita temukan apalagi di musim penghujan adalah adanya pantulan atau bayangan objek pada genangan air atau ketika detikers bercermin pada cermin di rumah.

Nah bentuk bayangan tersebut dapat dibahas melalui refleksi transformasi geometri.

Pengertian Refleksi

Refleksi adalah jenis transformasi geometri yang memindahkan setiap titik pada suatu bidang dengan menggunakan sifat bayangan cermin dari titik yang dipindahkan.

Dalam refleksi, bayangan yang ada di dalam cermin akan selalu sama dengan benda yang dicerminkan. Dengan demikian, pencerminan memiliki sifat yang sama dengan simetri lipat.

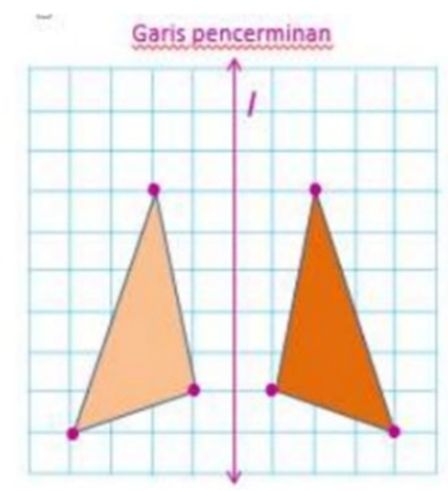Gambar refleksi Foto: Buku Kumpulan Materi Ajar Kreatif oleh Nanda Hidayat

Berdasarkan gambar di atas, ciri-ciri refleksi adalah:

• Bayangan suatu bangun yang dicerminkan memiliki bentuk dan ukuran yang sama dengan bangun yang aslinya.
• Jarak bayangan ke cermin sama dengan jarak benda aslinya ke cermin.
• Bayangan bangun pada cermin saling berhadapan dengan bangun aslinya.

Dari gambar tersebut, juga terlihat sifat-sifat refleksi yaitu:

• Sebuah ruas garis jika dicerminkan terhadap garis, maka panjang bayangannya sama dengan panjang garis itu.
• Pada pencerminan, titik atau garis yang tidak berpindah disebut titik atau garis invarian.
• Sebuah sudut dicerminkan terhadap sebuah garis mempunyai besar yang sama dengan sudut bayangnya.

Rumus Refleksi

Misalnya suatu segitiga PQR dicerminkan terhadap sumbu Y diperoleh bayangan P'Q'R'

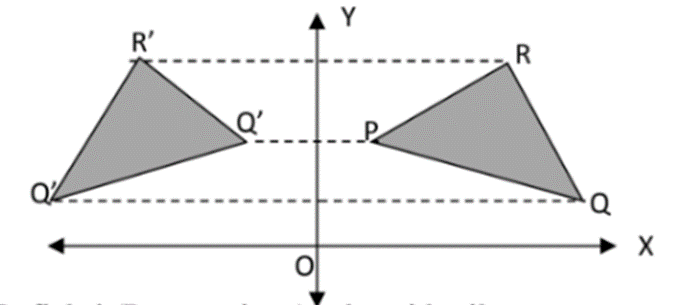Ilustrasi rumus refleksi Foto: Kumpulan Rumus dan Soal-soal Matematika oleh Budi Pangerti

1. Rumus Refleksi terhadap Sumbu X

Jika titik yang direfleksikan adalah (x, y), maka titik hasil refleksi adalah (x, -y). Pada gambar, dapat diambil kesimpulan bahwa P(x, y) pada sumbu X adalah P'(x,-y)

2. Rumus Refleksi terhadap sumbu Y

Jika titik direfleksikan (x,y) maka titik hasil refleksi adalah (-x, y). Pada gambar, dapat diambil kesimpulan bahwa P(x,y) pada sumbu Y adalah P'(-a, b).

3. Rumus Refleksi terhadap titik O (0,0)

Jika titik direfleksikan (x,y) maka titik refleksi adalah (-x,-y). Pada gambar, dapat diambil kesimpulan bahwa P(x,y) pada titik O (0,0) adalah P'(-x, -y)

4. Rumus Refleksi terhadap Garis y=x

Jika titik direfleksikan (x,y) maka titik refleksinya adalah (y,x). Pada gambar, dapat diambil kesimpulan bahwa P(x,y) pada garis y=x adalah P'(y,x)

5. Rumus Refleksi terhadap Garis y= -x

Jika titik direfleksikan (x,y) maka titik refleksinya adalah (-y, -x). Pada gambar, dapat diambil kesimpulan bahwa P(x,y) terhadap garis y=-x adalah P'(-y, -x).

6. Rumus Refleksi terhadap Garis x = h

Jika titik yang direfleksikan (x,y) maka titik refleksinya adalah (2h - x,y). Pada gambar, dapat disimpulkan bahwa P (x,y) terhadap garis x= h adalah P'(2h - x,y).

7. Rumus Refleksi terhadap Garis y = h

Jika titik yang direfleksikan (x,y) maka titik refleksinya adalah (x, 2h-y). Pada gambar, dapat diambil kesimpulan bahwa P (x,y) terhadap y=h adalah P'(x, 2h-y)

Contoh Soal Rumus Refleksi

1. Tentukan bayang titik A(6,-3) oleh pencerminan terhadap sumbu x adalah....

Jawaban

Pencerminan terhadap sumbu x

P (x,y)à P'(x, -y)

A(6, -3)à A' (6,3)

2. Tentukan bayang segitiga dengan S(-2, 4) , T(3,-7), U(6,5) oleh pencerminan terhadap sumbu y= -x....

Jawaban

Bayangan STU oleh s pencerminan terhadap sumbu y= -x adalah (x,y)à (-y,-x)

S(-2,4) à (-4,2)

S(3,-7) à (7,-3)

S(6,5) à (-5,-6)

3. Tentukan bayang dari garis y = -x+ 3 jika dicerminkan terhadap garis y= -x....

Jawaban

Persamaan dari pencerminan terhadap garis y = -x adalah x' =-y dan y' =-x, dari persamaan tersebut maka x = -y' dan y = -x'. Kemudian substitusi x dan y ke persamaan garis y = -x +3 sehingga diperoleh:

-x = -(-y') + 3

-x' = y' +3

Y' = x' - 3 buang tanda aksen sehingga diperoleh garis

Y = x-3

Demikian Penjelasan tentang rumus refleksi dan contoh soalnya. semoga dapat bermanfaat untuk detikers!